Problème de la "curva aequabilis pressionis" posé par Jean Bernoulli en 1695, résolu par L'Hospital en 1700. Autres noms : courbe de pression constante, courbe du looping.

 

Paramétrisation cartésienne :  où . La loi horaire du mouvement est donnée par : . Abscisse curviligne et rayon de courbure : .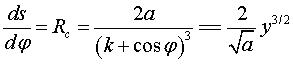

Pour k = 1 (cas de la quintique de l'Hospital) : Paramétrisation cartésienne :  (). Equation cartésienne :  ou . Quintique polynomiale. Sommet (0, a/4) ; point isolé  ;  point double . Abscisse curviligne : . Rayon de courbure : . Paramétrisation de la développée : .

Une courbe à réaction constante est une courbe telle que si une particule descend par gravité le long d'elle (le champ de gravitation étant considéré comme uniforme), la réaction de la courbe sur la particule conserve une intensité constante ; inversement, la force exercée par la particule sur la courbe est d'intensité constante.
 

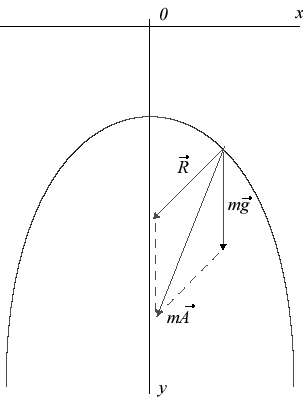En prenant Oy comme verticale descendante, la relation fondamentale de la dynamique, projetée sur la normale, s'écrit : , où R est l'intensité de la réaction du support, supposée constante (voir les notations). La conservation de l'énergie s'écrit : , en choisissant . Désignant par  le rapport de la réaction au poids du mobile, on obtient l'équation différentielle de la courbe : . Sa résolution (utiliser ) donne la paramétrisation indiquée ci-dessus. Attention, la courbe déterminée n'est à réaction constante que pour une seule valeur de la vitesse au sommet : .

 

	Dans le cas k > 1,  la courbe est transcendante, ( s'intègre à l'aide de fonctions circulaires réciproques) ; on obtient une courbe périodique.
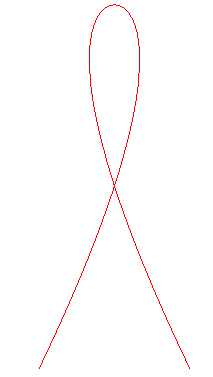
voir figure dans l'encadré violet	Dans le cas k = 1, la courbe est algébrique ; c'est le seul exemple de courbe remarquable de degré 5 de ce site.
	Dans le cas k < 1,  la courbe est de nouveau transcendante ( s'intègre à l'aide de fonctions hyperboliques réciproques).

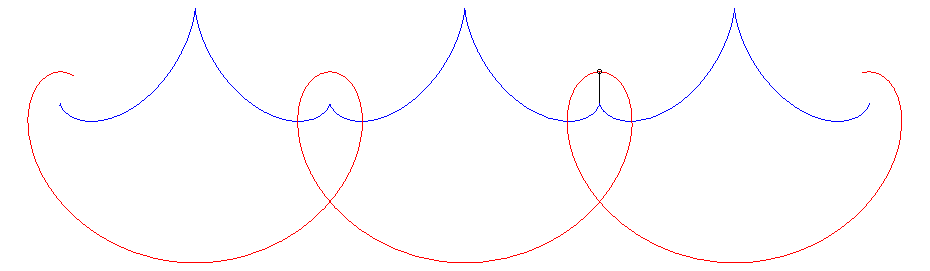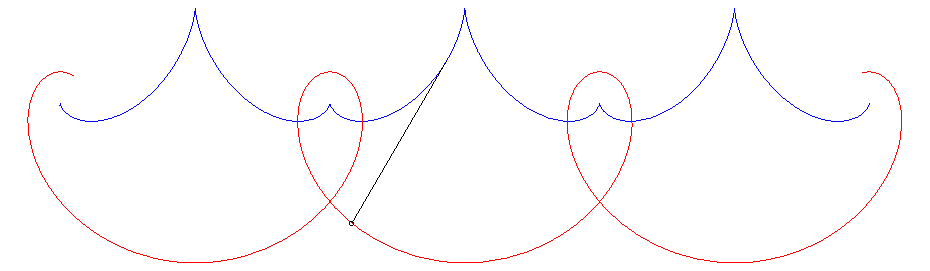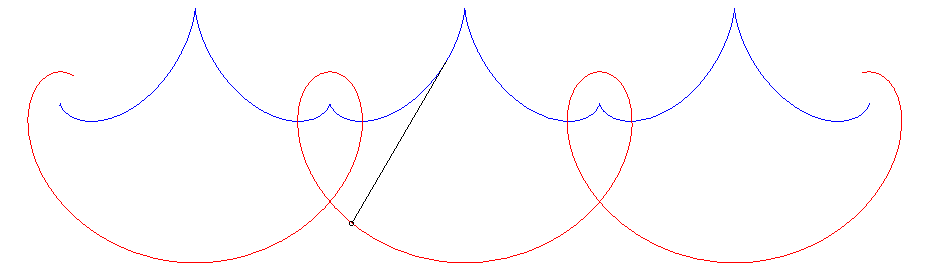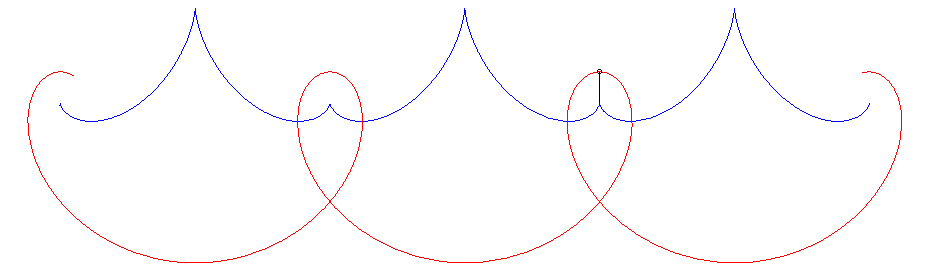
La développée d'une telle courbe donne la solution au problème suivant (également posé par Jean Bernoulli) : déterminer une courbe sur laquelle enrouler le fil d'un pendule de sorte que la tension du fil de ce pendule reste constante.
 

Pendule à tension constante ; en rouge la courbe à réaction constante, en bleu, sa développée.

Pour d'autres courbes de mouvement d'un point matériel dans un champ de pesanteur soumises à certaines conditions, voir à  isochrone, brachistochrone et tautochrone.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Jacques MANDONNET 2003